
(4)
M. Chen, X. Guo, M. Farag, N. Qian, X. Song, A. Ni, V. Liu, X. Yu, Y. Ma, L. Yang, W. Yu, M. King, J. Lee, R. Zare, W. Min, R. Pappu, Y. Dai
“Condenzymes: Biomolecular condensates with inherent catalytic activities”.
bioRxiv 10.1101/2024.07.06.602359




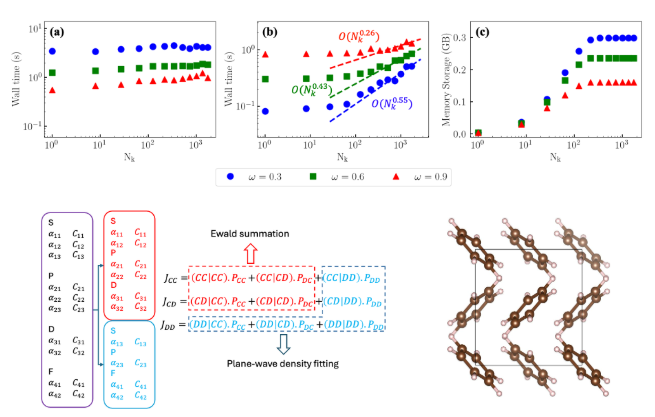
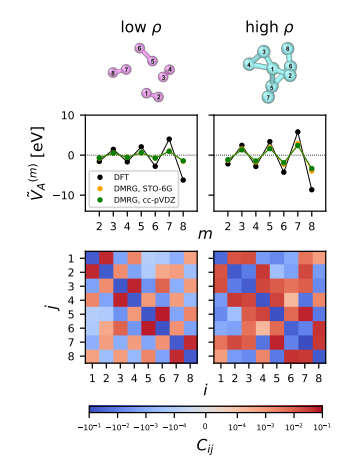

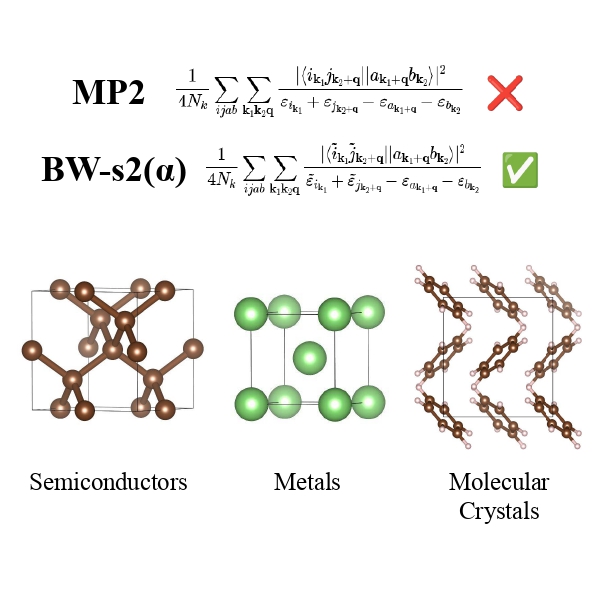
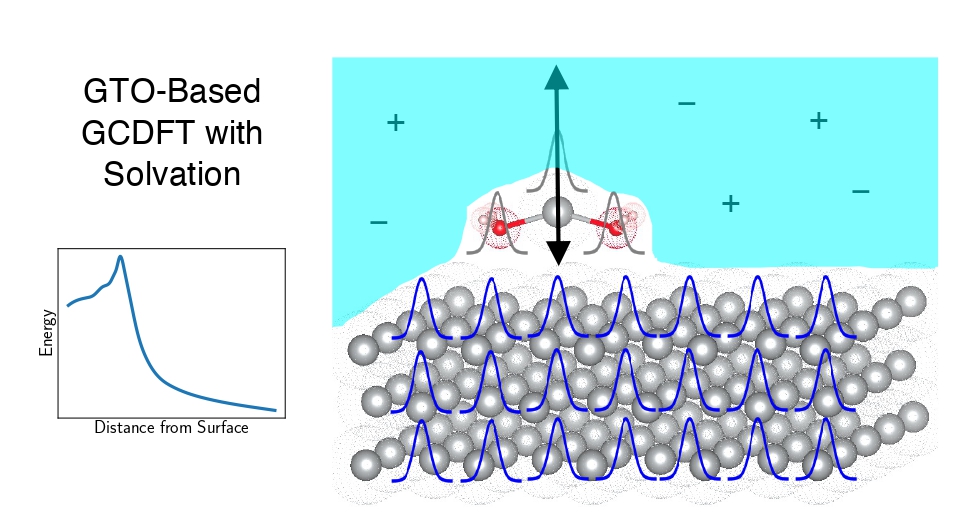
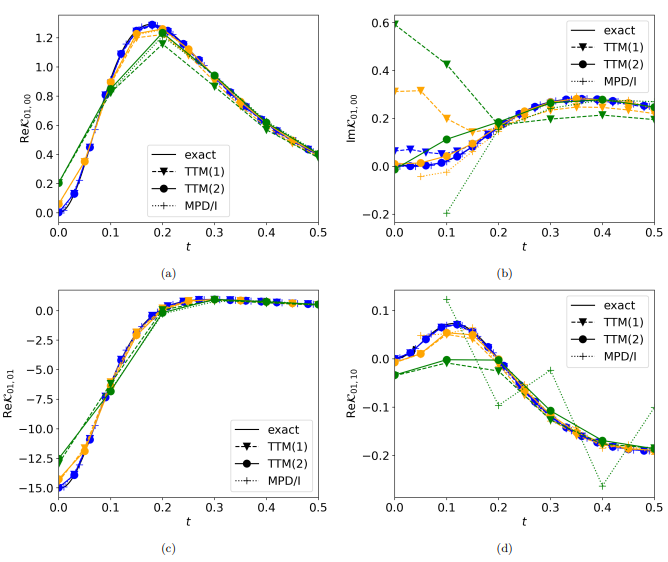
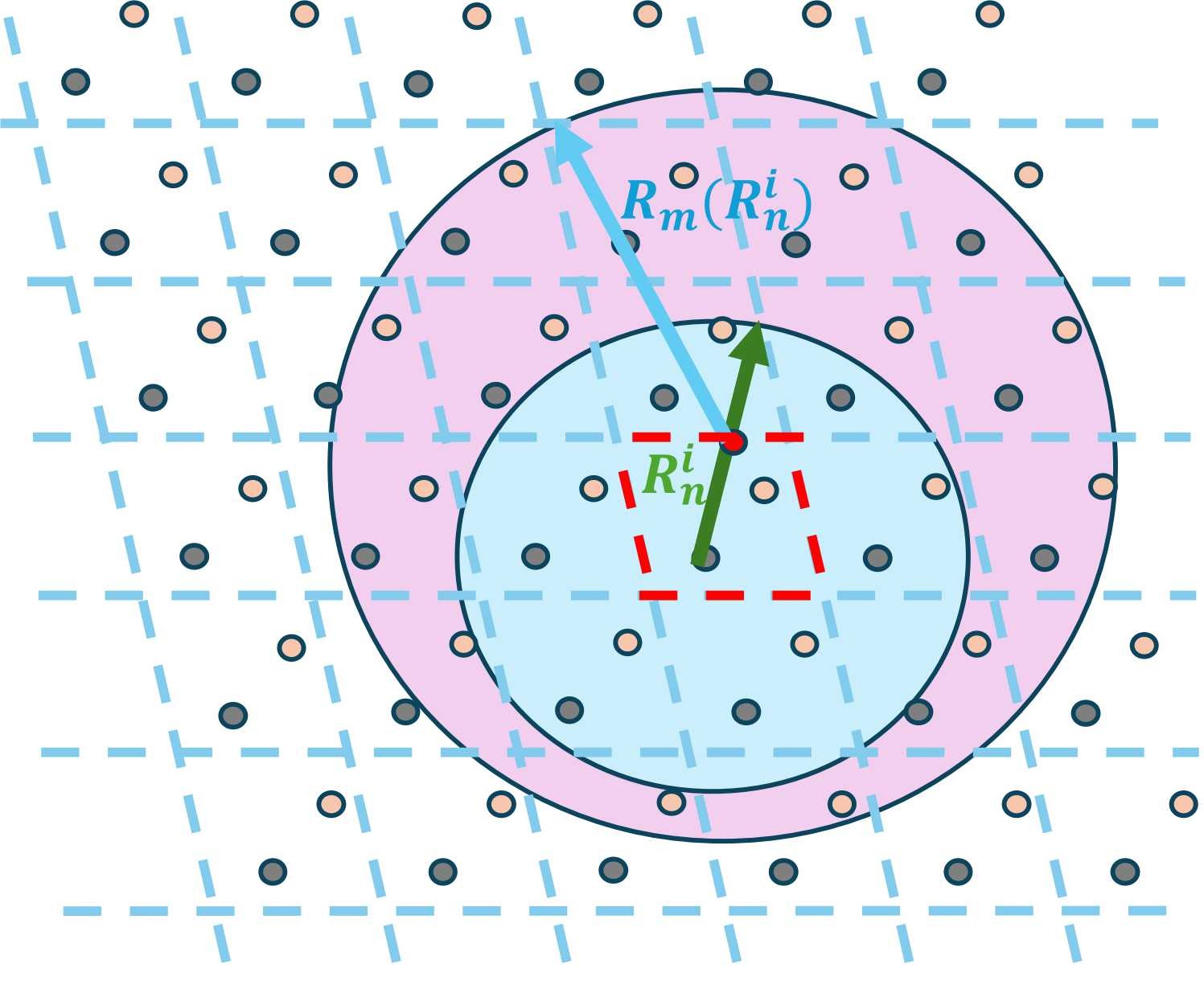
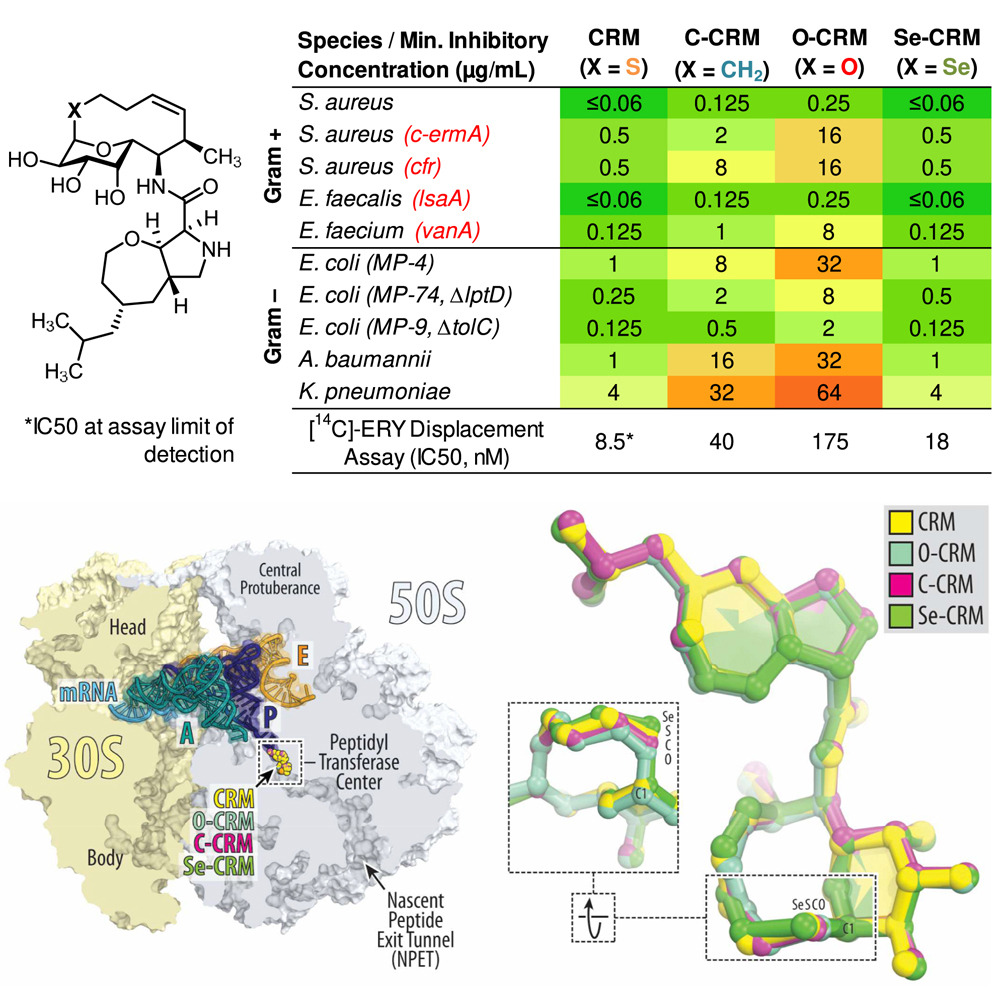

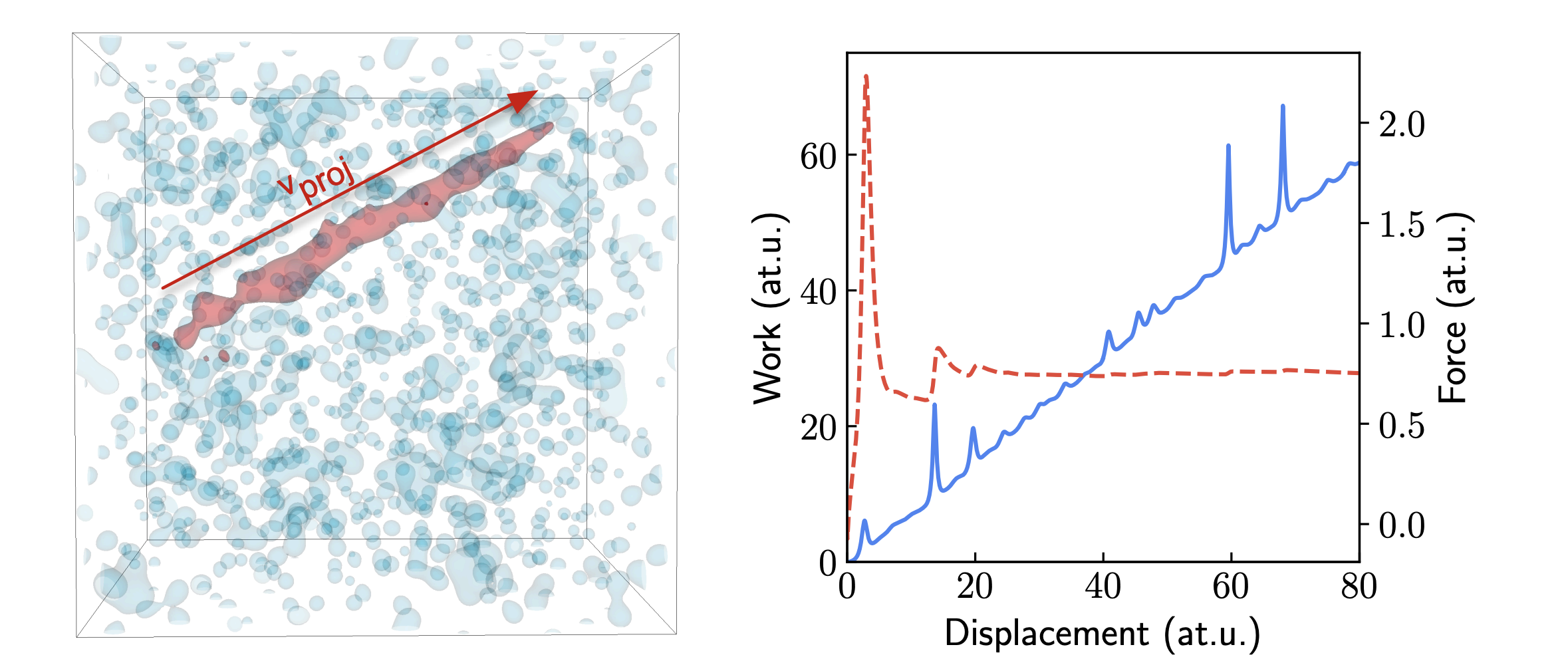
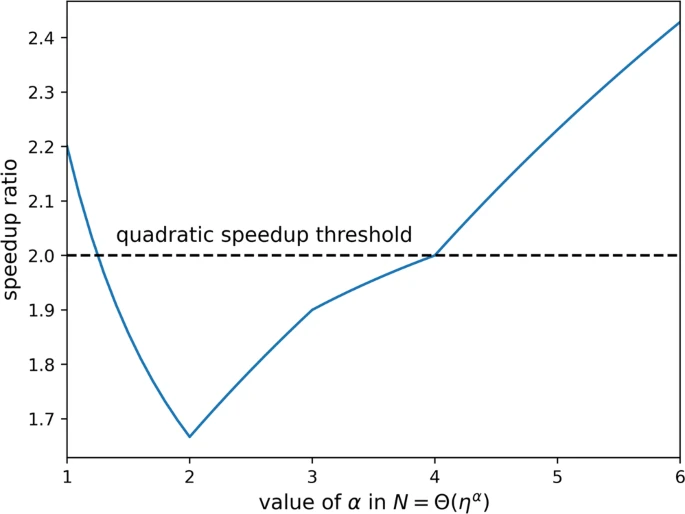
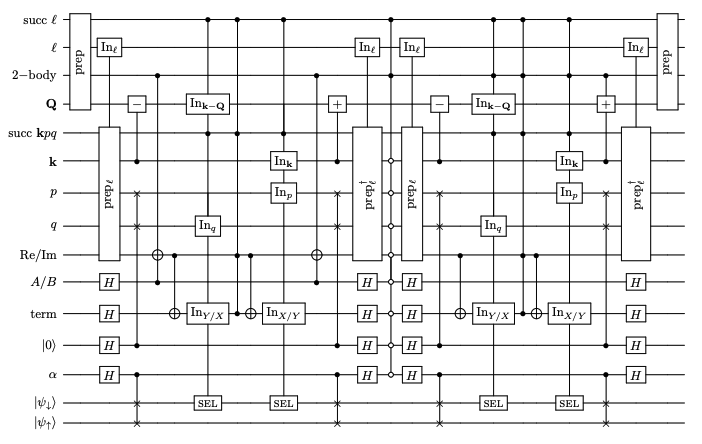
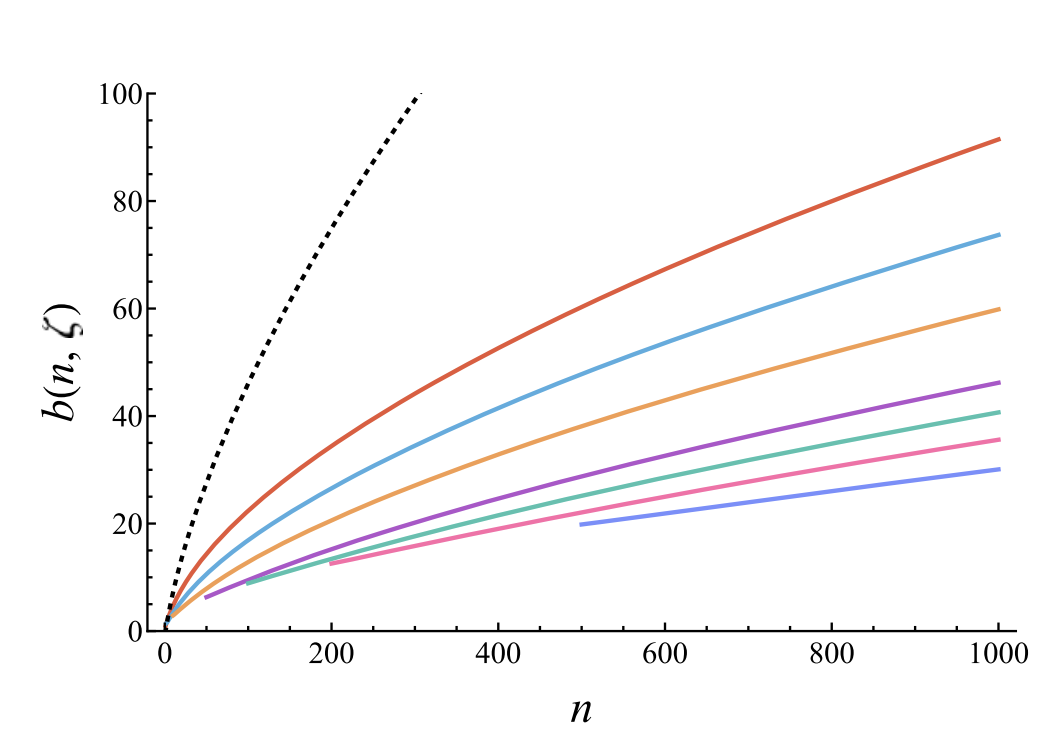
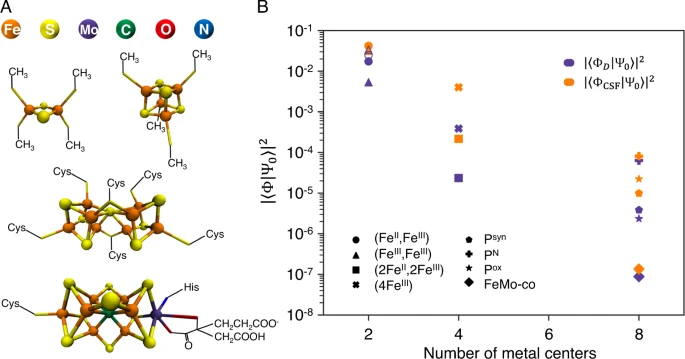

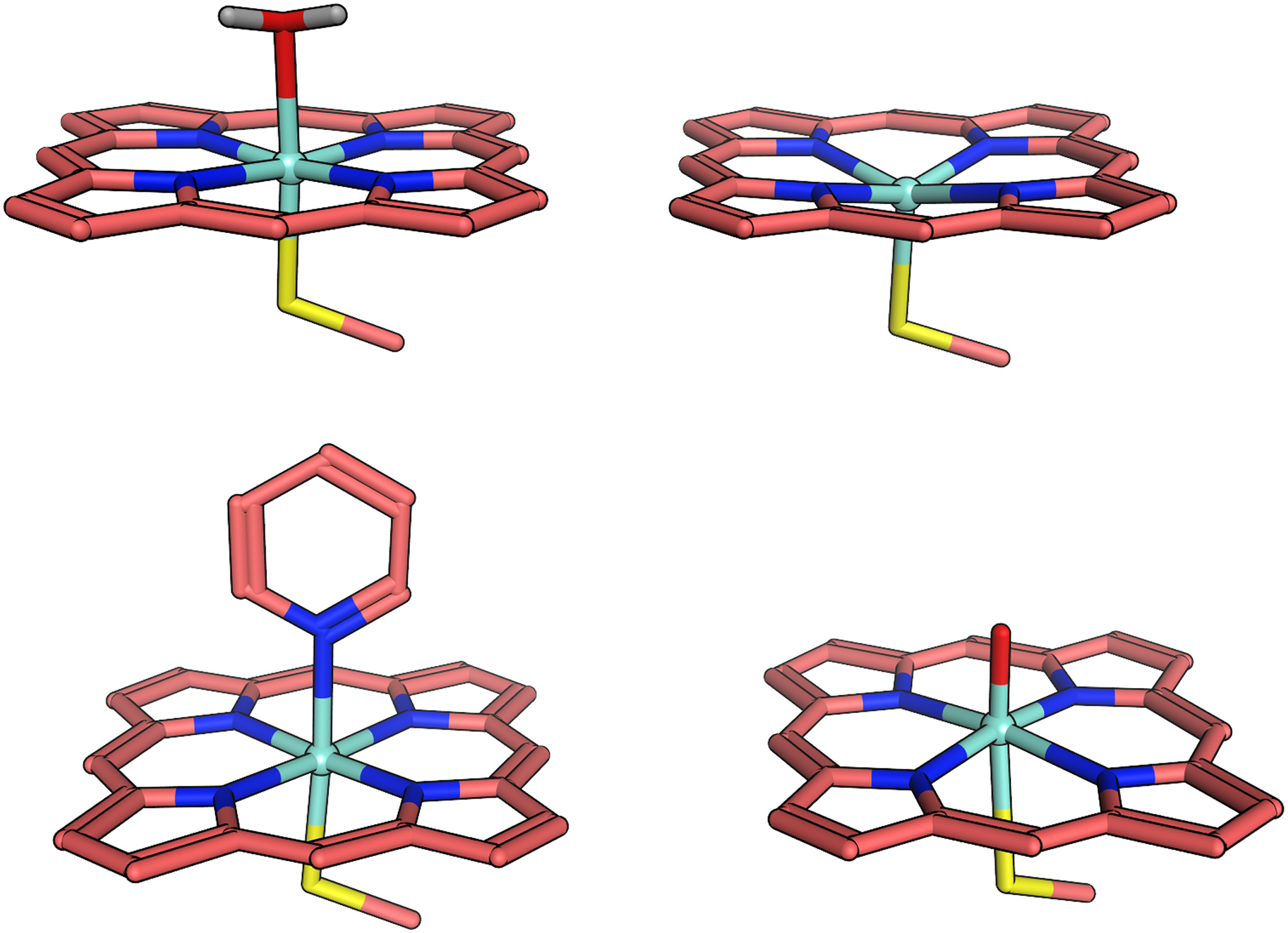
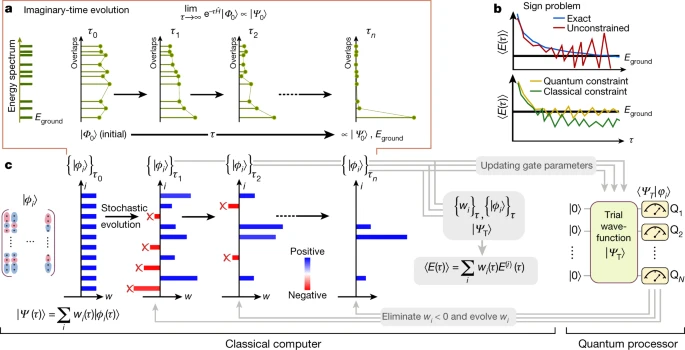

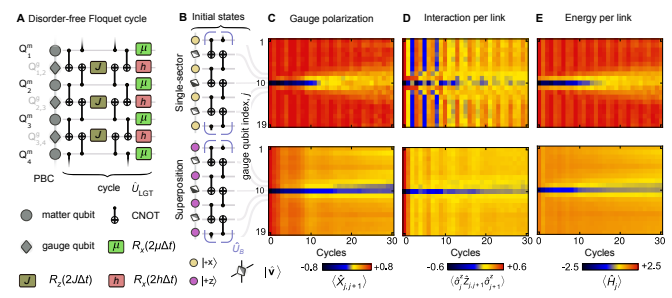
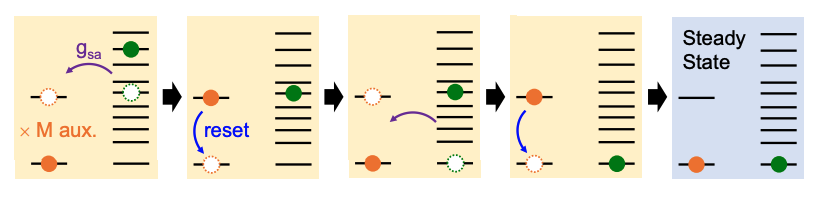
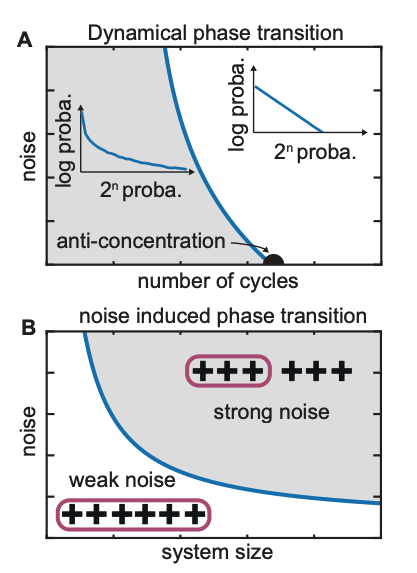


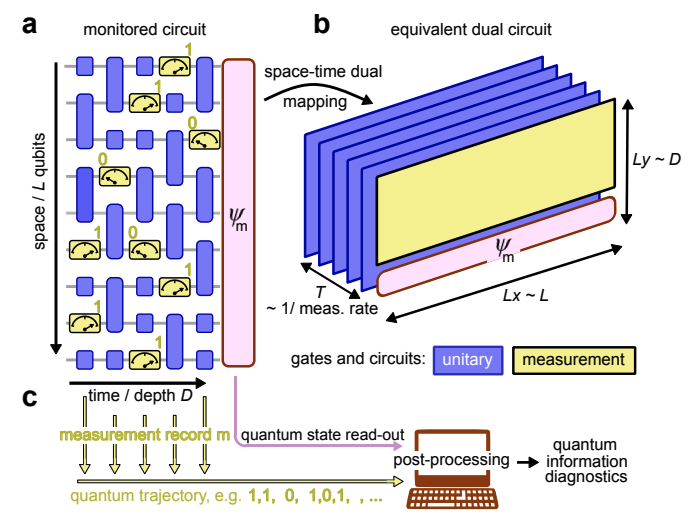
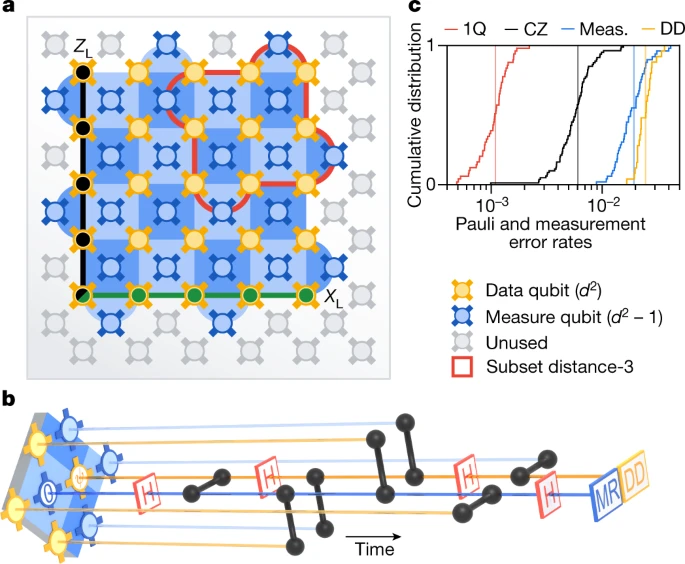



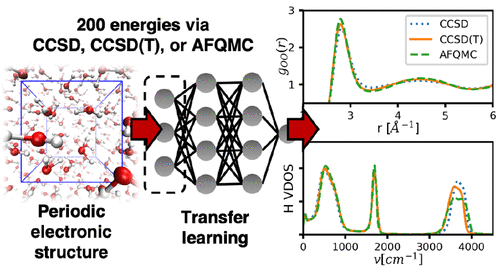
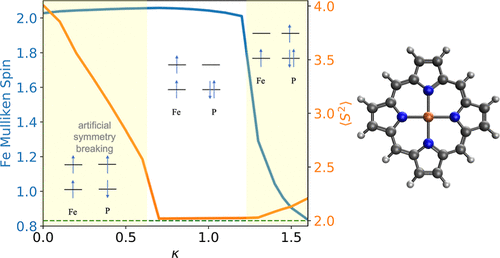
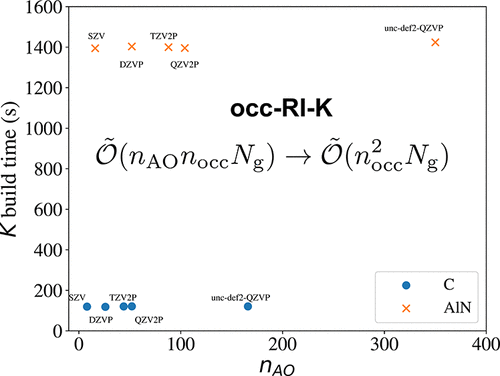
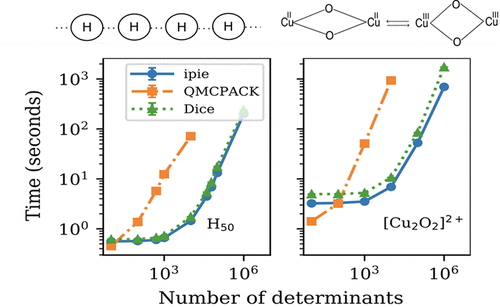
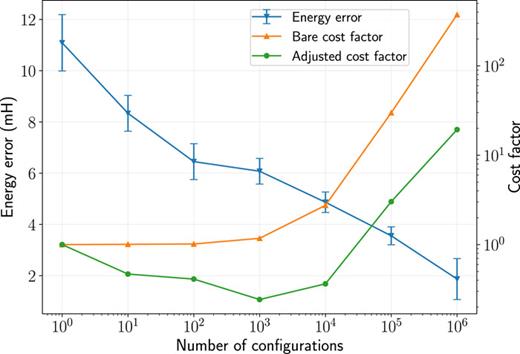
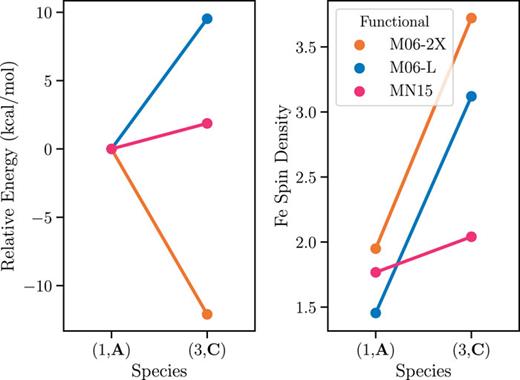

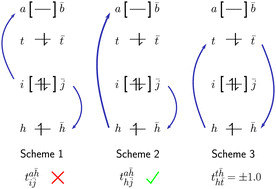
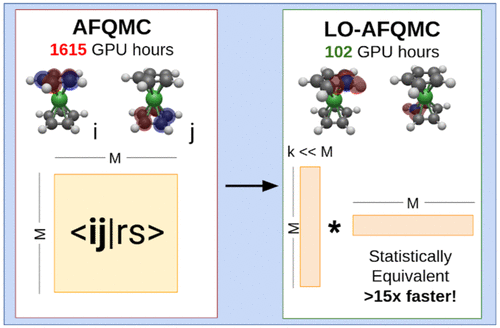
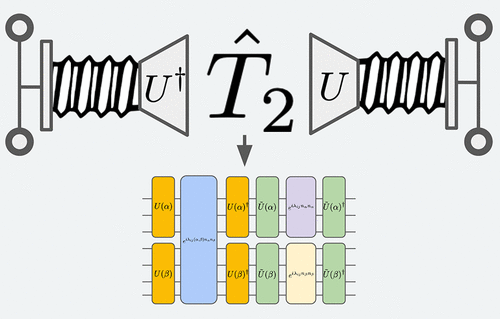
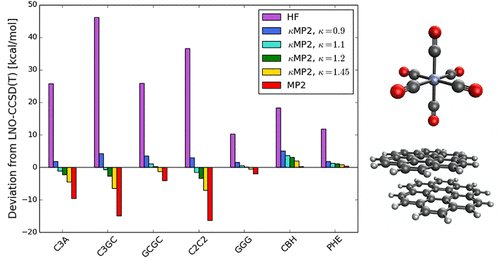
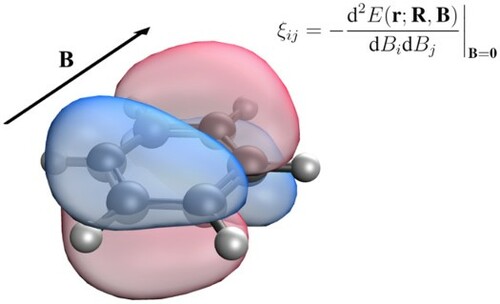
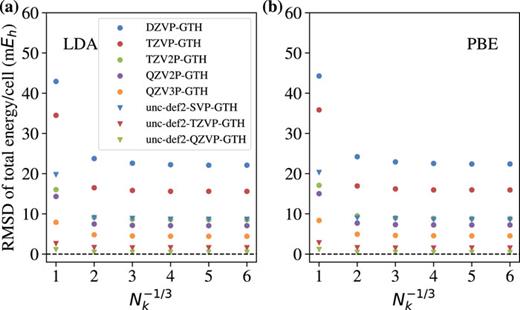
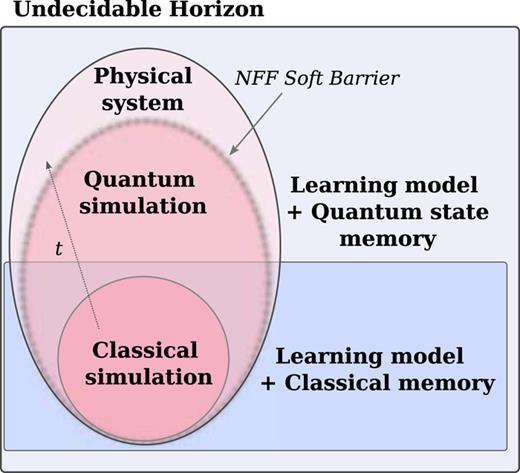
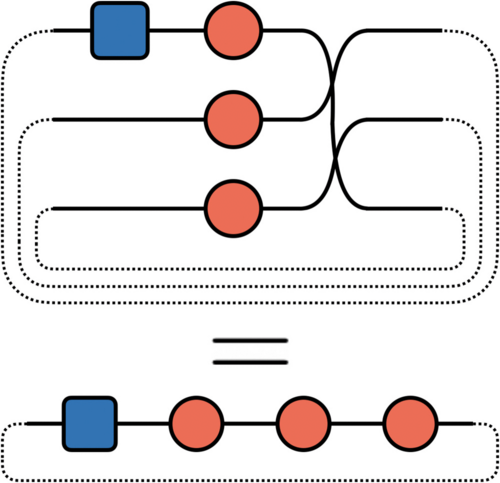
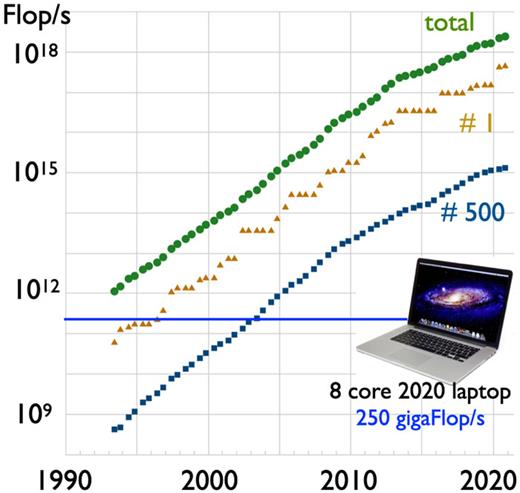
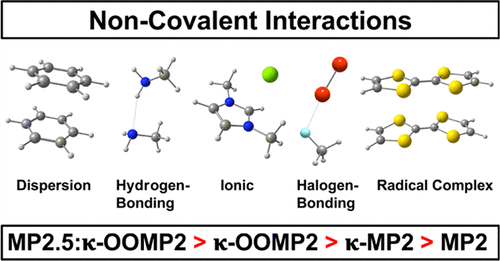
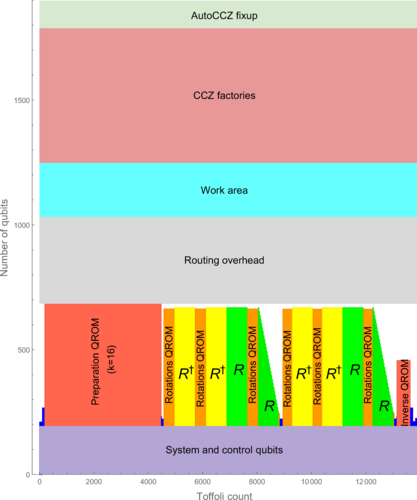
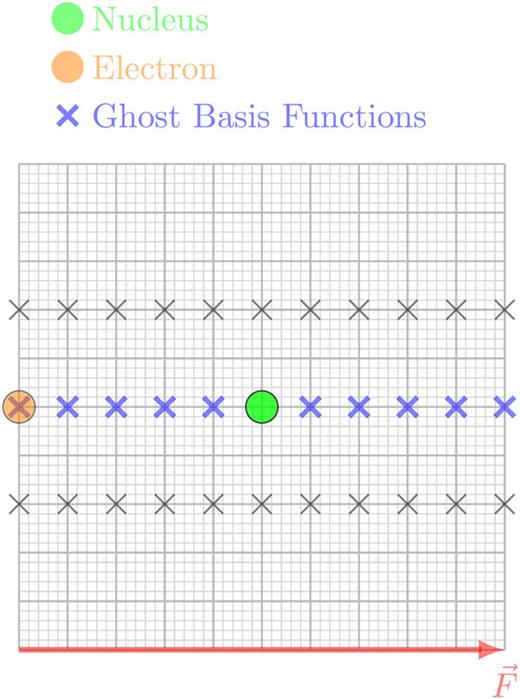
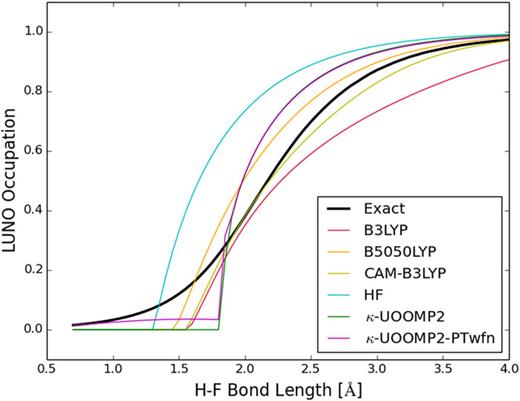
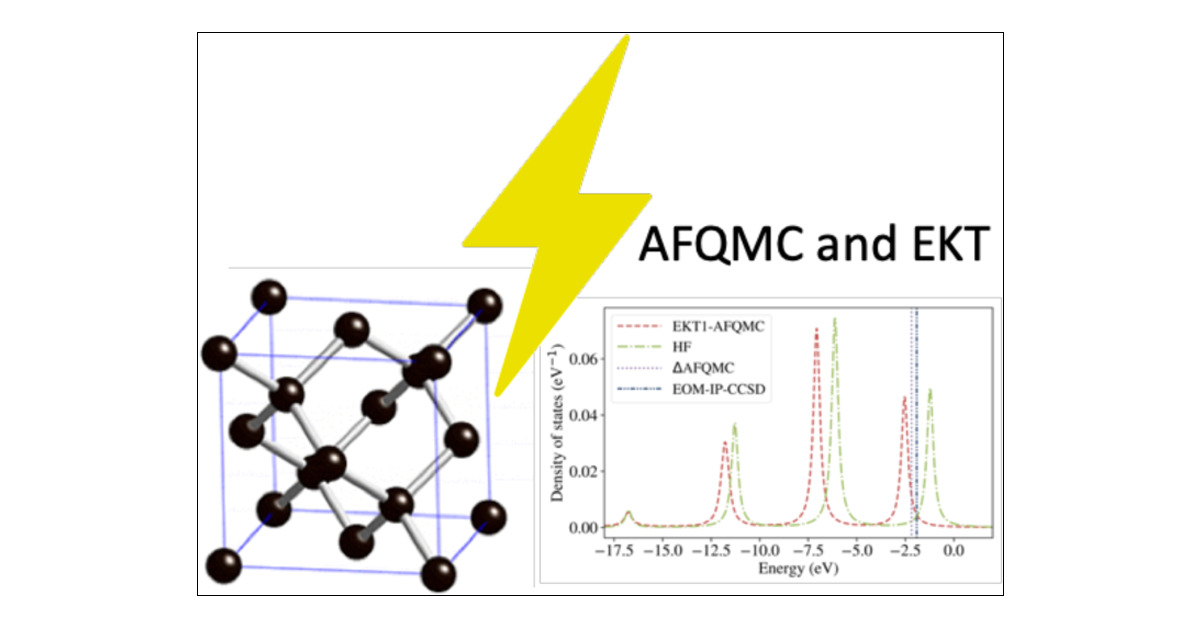
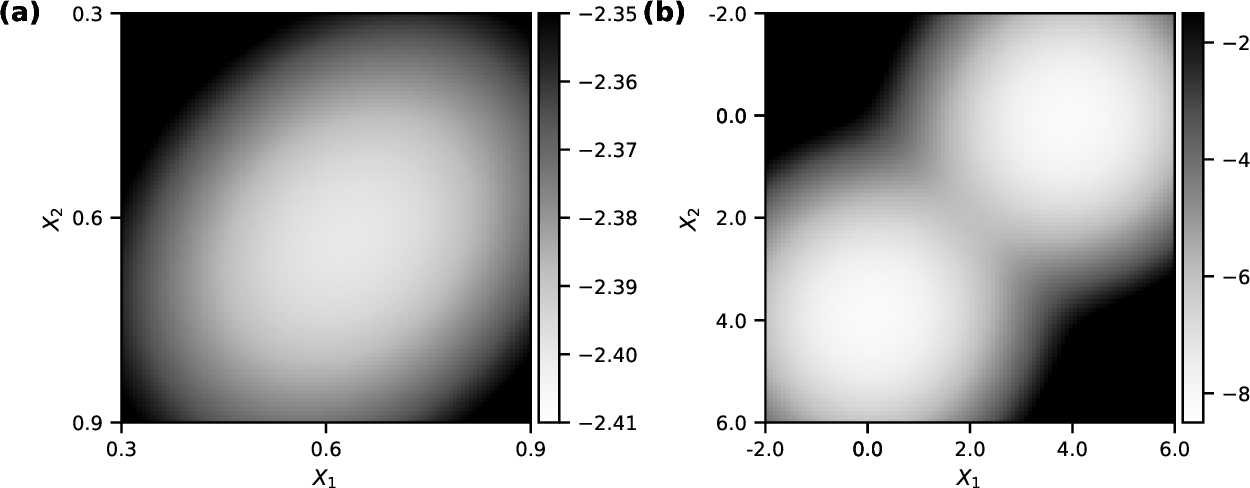
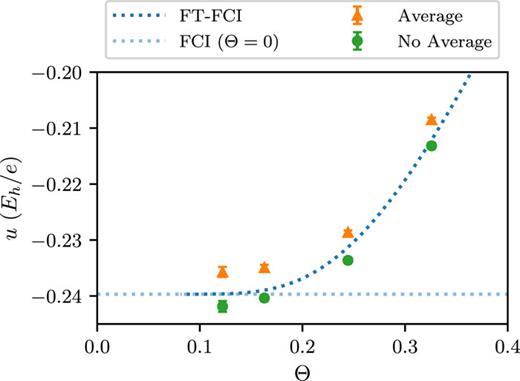
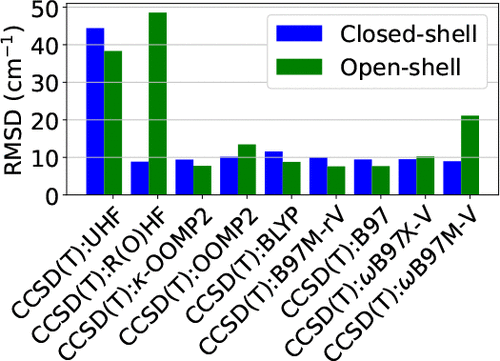
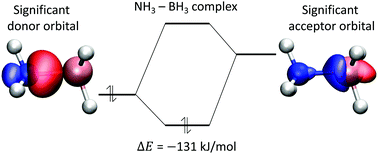
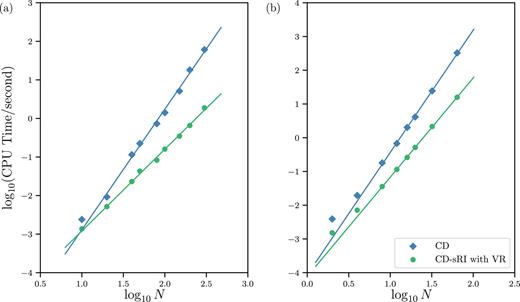
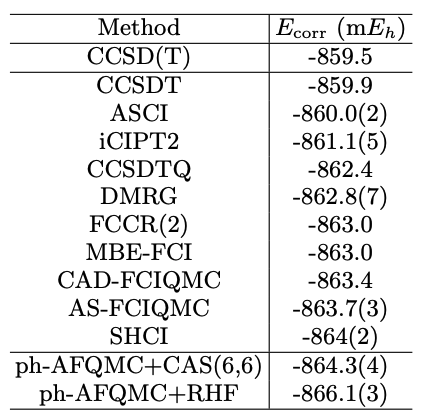
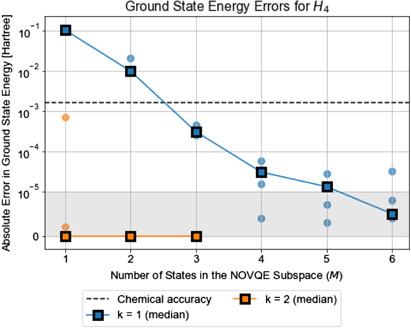
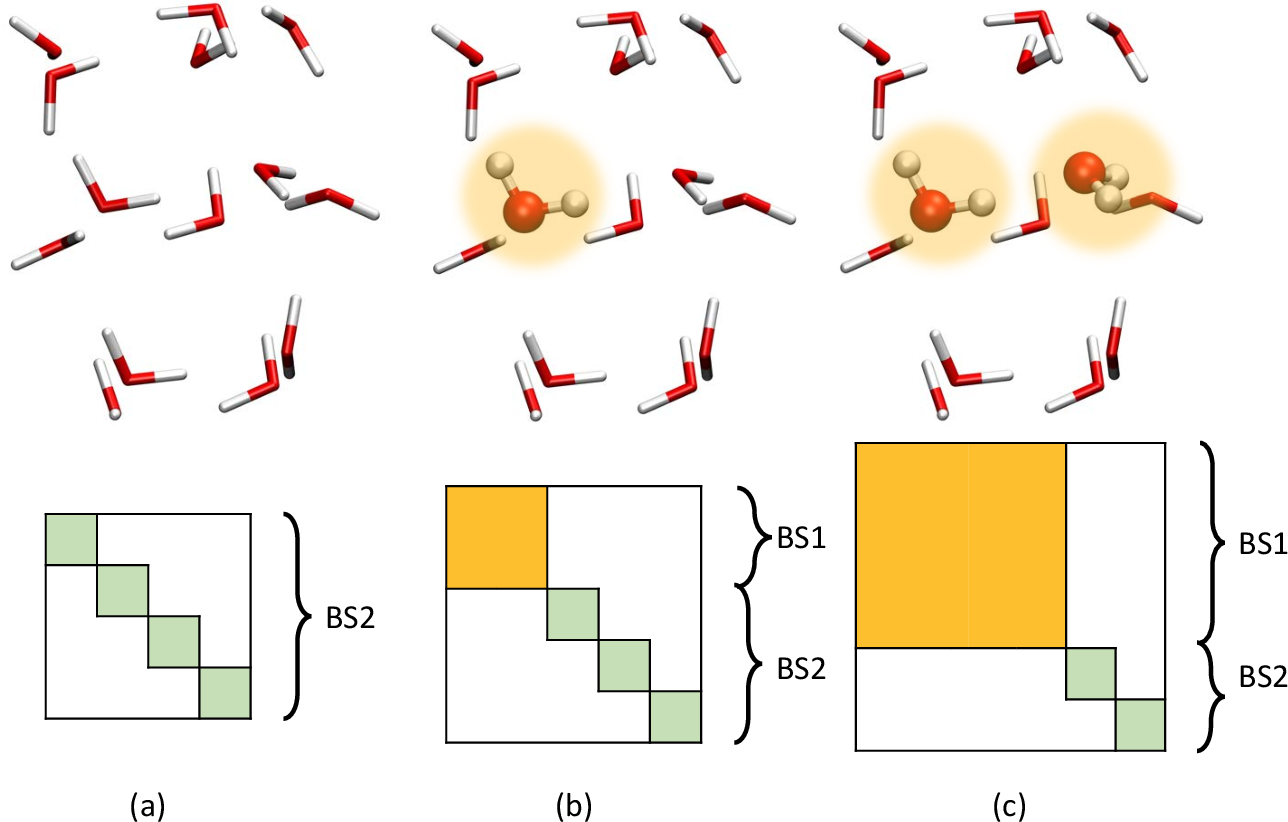

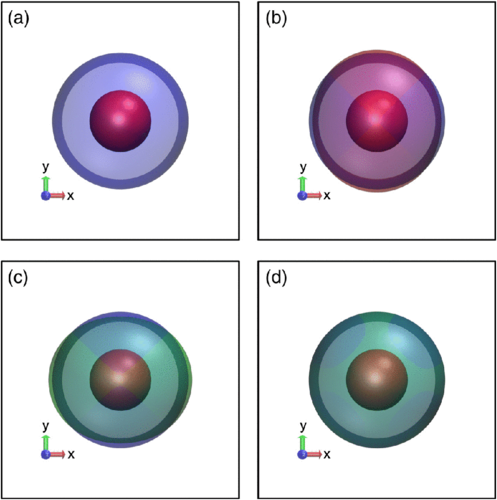
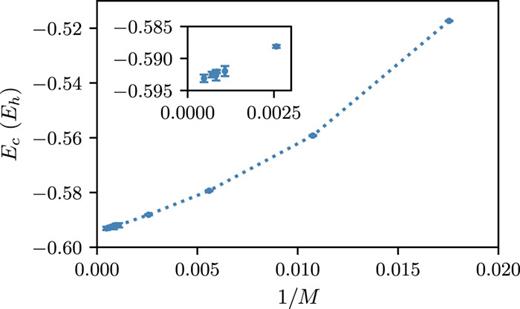
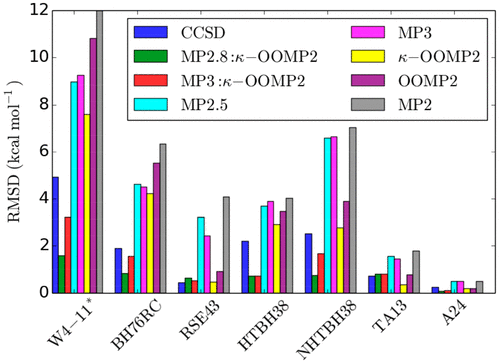
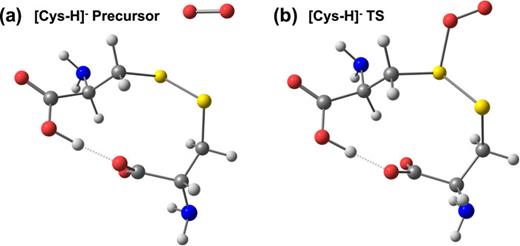
.gif)
.gif)
.jpeg)
.gif)
.gif)
.gif)
.gif)
.jpeg)
.gif)
.png)
.gif)